浮点数转换问题与操作指令
一直对于计算机的浮点数操作原理以及指令很模糊,特别是关于浮点数操作的汇编指令以及寄存器方面的知识,这里记录下(所使用的标准是IEEE754)
关于浮点数在内存中的存储
下面的图是32位浮点数与64位浮点数在内存中的存储形式,和计算公式
如果exp全为1就代表无限大或者NaN(not a number),如果exp全为0代表非规格化
随后在引入一个概念Bias,计算公式为:Bias = 2k-1-1,其中k等于exp所占的二进制位数(32位的浮点数占8位,64位的浮点数占11位)32位的Bisa=127,64位的Bisa=1023
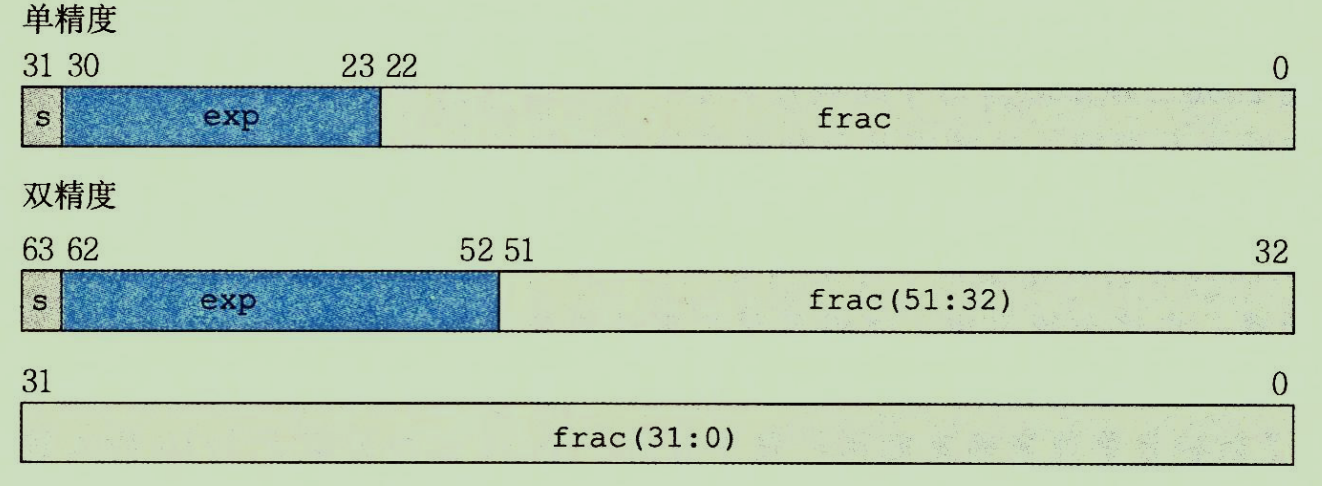
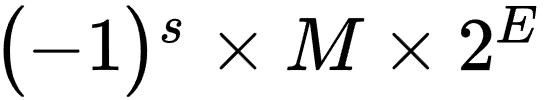
浮点数在内存中的存储分为三段:
- 符号位S
- 阶码E
- 尾数M
理清E,exp,Biased三者的关系
三者的计算公式为E = exp - Biased(特别的,如果exp等于0,则公式变为E = 1 - Biased)
一定要注意阶码E不会直接存在内存中,而是通过上面的计算将阶码E转化为exp存放在内存中
举两个例子
将数12345转化为浮点数的16进制形式(用32位为例子)
首先将12345转化为二进制数形式
1
12345 = (11000000111001)2
得到12345 = (1.1000000111001)2 x 213,那么现在尾数就是1.1000000111001,将小数点前面的1舍去,后面补0直到长度为23位得到尾数M的二进制表示形式,还有阶码E=13
1
10000001110010000000000
计算exp
计算的数字是32位的,通过上面计算得到阶码E=13,在通过公式exp=E+Biased,得到exp=13+127=140
1
140 = (10001100)2
将三者组合
1
20 10001100 10000001110010000000000
s exp frac1
(01000110010000001110010000000000)2 = 0x4640E400
将1.8转化为浮点数的16进制形式(用32位为例)
将1.8转化为二进制形式
1
1.8 = (1.11001100110011001100110)2
由于1.8转化为二进制是一个无线循环的数字,所以取前23位并向前进一位
这里阶码E=0
计算exp
公式exp=E+Biased,得到exp=0+127
1
127 = (01111111)2
将三者组合
1
(00111111111001100110011001100116)2 = 0x3FE66666
验证
使用gdb调试看看是否是这样存储在内存中,使用命令gcc -g -m32 check.c -o check编译
1 |
|
1 | 0x565561ce <main+34> push dword ptr [ebp - 4] |
可以看到和上面计算的值是一样的,64位的双精度浮点数也是这样计算
浮点数操作常用指令
现在使用的很多浮点数都是双精度浮点数,官方也推荐使用双精度浮点数
- 移动指令
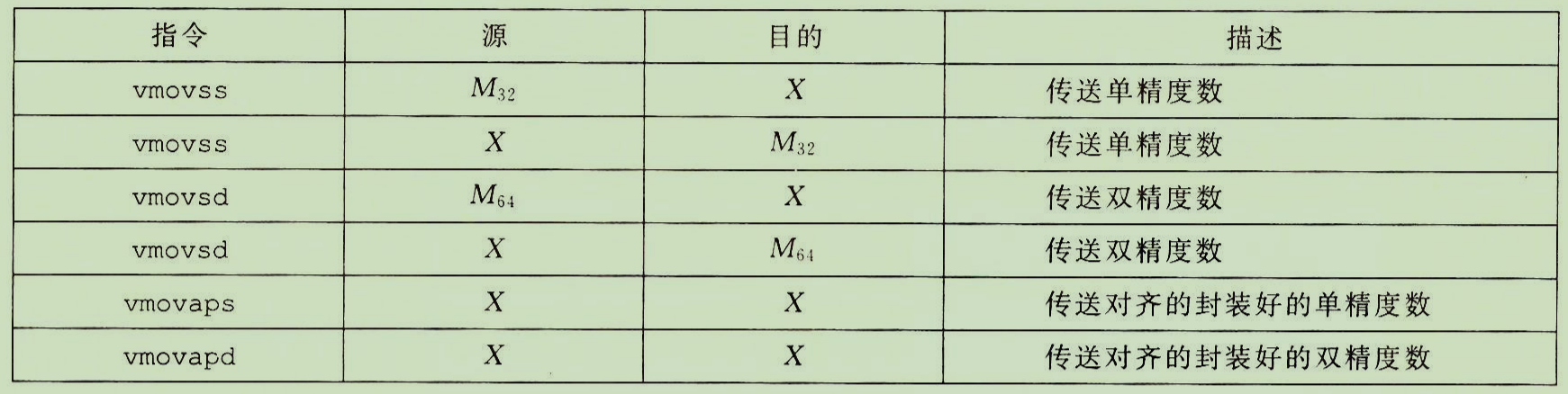
- 浮点数转整形指令

- 整形转浮点型指令

- 浮点数操作运算