cache lab

前言

这章从看视频到看书再到做lab用了小一个星期的时间，做得怀疑智商，cachelab中的PartB部分只能勉强搞懂，还得看网上大佬的思路，算了不少草稿才勉强将miss次数给算出来，看到后面还有更难的lab已经开始害怕了。由于时间问题，这个lab没有研究到满分（及格都够呛）

实验文件介绍

├── cachelab.c
├── cachelab.h
├── csim.c
├── csim-ref
├── driver.py
├── Makefile
├── README
├── test-csim
├── test-trans.c
├── tracegen.c
├── traces
│   ├── dave.trace
│   ├── long.trace
│   ├── trans.trace
│   ├── yi2.trace
│   └── yi.trace
└── trans.c

csim.c和trans.c文件，前一个文件是需要我们实现一个缓存模拟器，第二个是实现矩阵转置

test-csim文件：测试我们写的缓存模拟器

csim-ref：我们所写的缓存模拟器样例，要求和这个一模一样

test-trans.c：在编译过后测试矩阵

driver.py：当所有部分都完成后计算出所得分数

cachelab Part A

这一关让我们写一个缓存模拟器（高级学生管理系统），在进行组内行置换时使用LRU算法。比较简单，说下cache的数据结构和关键代码就行，完整代码放在了github

// cache结构体定义
typedef struct Cache {
    CacheLinkList **linkListArr;
    CacheInfo *cacheInfo;
    U64 *cacheLineCount;
}Cache;

结构体中使用了一个数组指针记录了每一组的头节点，CacheInfo记录了cache的基本数据，在定义一个数组记录每一组行好使用LRU算法进行页面置换，每一组的使用了双向链表来进行链接。

//cache剩余结构体定义如下
typedef struct CacheInfo {
    U64 sets;
    U64 lines;
    U64 blockSize;
}CacheInfo;

typedef struct CacheLinkList {
    CacheLine *cacheLine;
    struct CacheLinkList *prev;
    struct CacheLinkList *next;
}CacheLinkList;

typedef struct CacheLine {
    U64 sign;
    U64 tag;
    U8 *block;
} CacheLine;

我还将从文件读取的地址也放在了结构体中，地址部分的结构体定义如下

//存放地址的结构体定义
typedef struct AddInfo {
    //address mark struct
    U64 t;
    U64 s;
    U64 b;
} AddInfo;

typedef struct Address {
    char op;
    U64 add;
    U64 size;
    AddInfo *addInfo;
} Address;

typedef struct AddLinkList {
    Address *address;
    struct AddLinkList *prev;
    struct AddLinkList *next;
}AddLinkList;

在计算是否命中时，使用如下思路，首先判断存放组链表表头的地址是否为空，如果为空就添加然后返回MISS

CacheLinkList *head = cache->linkListArr[set];

    // first match if success return hit
    if (head == 0) {
        head = (CacheLinkList*) malloc(sizeof(CacheLinkList));
        cache->linkListArr[set] = head;
        CacheLine* cacheLine = (CacheLine*)malloc(sizeof(CacheLine));
        head->cacheLine = cacheLine;
        head->next = 0;
        head->prev = 0;
        head->cacheLine->sign = 1;
        head->cacheLine->tag = tag;
        head->cacheLine->block = 0;
        cache->cacheLineCount[set]++;
        return MISS;
    }

如果表头不为空，就遍历这个双向链表，判断tag是否匹配，如果匹配到tag，就判断这个节点是头节点，尾节点，或者中间的节点，然后将这个命中的节点变成表头节点，返回HIT。

while(node != 0) {
        if(node->cacheLine->tag == tag) {
            if (node->prev == 0) {
                // first node
                cache->linkListArr[set] = node;
            }
            else if (node->next == 0) {
                // last node
                lastNode = node->prev;
                lastNode->next = 0;
                head->prev = node;
                node->next = head;
                node->prev = 0;
                cache->linkListArr[set] = node;
            }
            else {
                node->prev->next = node->next;
                node->next->prev = node->prev;
                head->prev = node;
                node->next = head;
                node->prev = 0;
                cache->linkListArr[set] = node;
            }
            return HIT;
        }
        lastNode = node;
        node = node->next;
    }

如果在遍历链表时没有命中tag，就判断这个组中的line是否已经满员，如果不满员，就添加一个新节点为表头，返回MISS

if (lineCount < lines) {
        // add to link list last
        newNode = (CacheLinkList*)malloc(sizeof(CacheLinkList));
        CacheLine* cacheLine = (CacheLine*)malloc(sizeof(CacheLine));
        newNode->cacheLine = cacheLine;
        newNode->cacheLine->sign = 1;
        newNode->cacheLine->tag = tag;

        newNode->next = head;
        newNode->prev = 0;
        head->prev = newNode;
        cache->linkListArr[set] = newNode;
        cache->cacheLineCount[set]++;
        return MISS;
    }

如果组中满员，就删除最后一个节点，然后添加新节点

newNode = (CacheLinkList*) malloc(sizeof(CacheLinkList));
    CacheLine* cacheLine = (CacheLine*)malloc(sizeof(CacheLine));
    memset(newNode, 0, sizeof (CacheLinkList));
    memset(cacheLine, 0, sizeof(CacheLine));
    newNode->cacheLine = cacheLine;
    newNode->cacheLine->tag = tag;

    if (lastNode->prev == 0) {
        cache->linkListArr[set] = newNode;
        free(lastNode->cacheLine);
        free(lastNode);
    }
    else {
        lastNode = lastNode->prev;
        free(lastNode->next->cacheLine);
        free(lastNode->next);
        lastNode->next = 0;
        newNode->next = head;
        newNode->prev = 0;
        head->prev = newNode;
        cache->linkListArr[set] = newNode;
    }

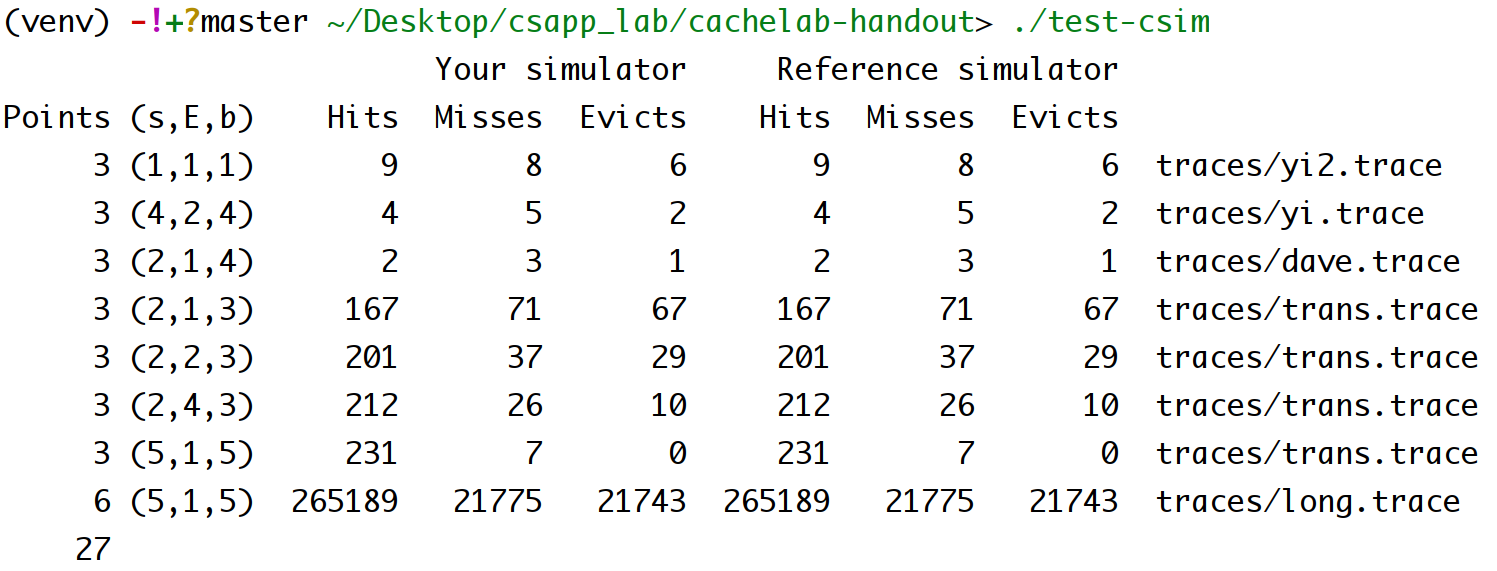
最后结果如下图

cachelab Part B

首先这一关的要求是最多使用12个局部变量，并且不能使用数据或者malloc函数申请内存来存放矩阵中的值，还不能使用递归算法

实现一个高hit低miss的矩阵转置，这一部分很考验想象力。由于测试用的矩阵太大不好画图，就先用4*4的矩阵讲解，首先放两个不同的矩阵转置代码和他们的命中率。

//高命中率转置代码
int i, j, k, l;
int v1, v2, v3, v4, v5, v6, v7, v8;
for (i = 0; i < N; i+=2) {
            v1 = A[i][0];v2 = A[i][1];v3 = A[i][2];v4 = A[i][3];
            v5 = A[i+1][0];v6 = A[i+1][1];v7 = A[i+1][2];v8 = A[i+1][3];
            B[0][i] = v1;B[1][i] = v2;B[2][i] = v3;B[3][i] = v4;
            B[0][i+1] = v5;B[1][i+1] = v6;B[2][i+1] = v7;B[3][i+1] = v8;
        }

//低命中率转置代码
int i, j, tmp;

    for (i = 0; i < N; i++) {
        for (j = 0; j < M; j++) {
            tmp = A[i][j];
            B[j][i] = tmp;
        }
    }    

他们两个的效率相差如下

这里使用缓存是(s, E, b) -> (5, 1, 5)，所以一共有32组，每组有一列缓存，每列缓存可以存放的字节大小为32

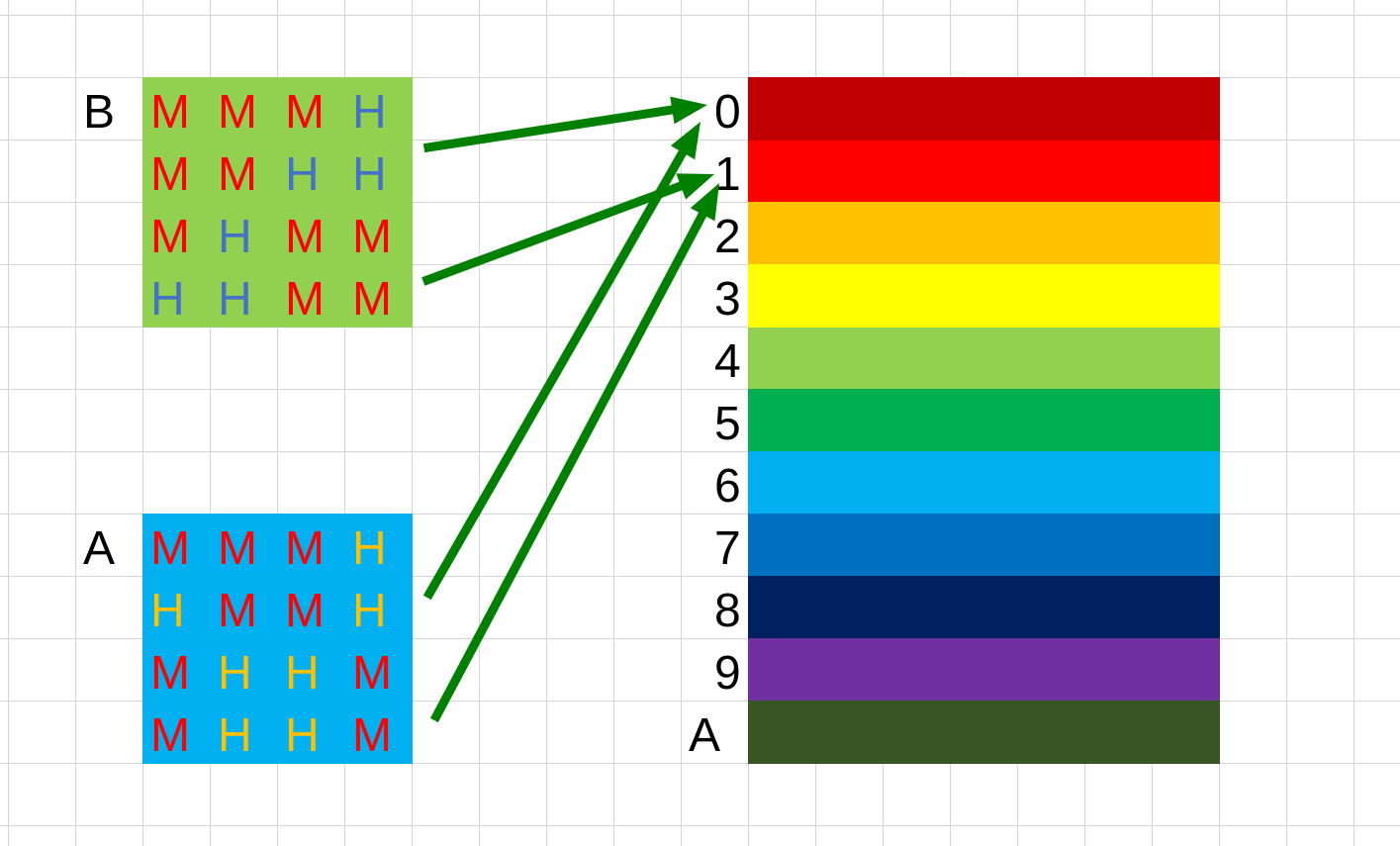
说下这8次miss和21次miss是怎么来的吧，先说普通的22次，这22次中有3次是系统miss，这是无法避免的。剩下就还有19次MISS，矩阵中的HIT与MISS分布图如下。

上面知道一个块最多有32个字节，也就能容纳8个int型整数，所以在4*4的矩阵中A和B的前两排都是映射到同一个组中，所以会造成这个情况。在优化以后，当A把矩阵中的两排也就是8个int数据读入缓存时，我们直接用局部变量将他读出来，这样就减少了缓存中的数据一直在A和B之间交换的情况，大大提高了缓存命中率。

优化后的转置A矩阵只有2次 MISS，B矩阵有3次MISS，加上系统的3次MISS，一共就是8次MISS。

32 x 32

一行有32个int型数据，假设将缓存中的数据全部填满，需要8行，也就是说这个矩阵中平均8行造成一次组映射冲突。这里采用一种分快技术，将一个32 x 32的矩阵，分成16个8 x 8的矩阵，然后使用在4 x 4矩阵中所使用的技术：每访问一次矩阵A，就将缓存中A的内容全部读取到局部变量中。

int i, j, k, l;
int v1, v2, v3, v4, v5, v6, v7, v8;
   if (N == 32) {
       for (i = 0; i < N; i += 8) {
           for (j = 0; j < M; j += 8) {
               for (k = i; k < i + 8; ++k) {
                   v1 = A[k][j + 0];
                   v2 = A[k][j + 1];
                   v3 = A[k][j + 2];
                   v4 = A[k][j + 3];
                   v5 = A[k][j + 4];
                   v6 = A[k][j + 5];
                   v7 = A[k][j + 6];
                   v8 = A[k][j + 7];
                   B[j + 0][k] = v1;
                   B[j + 1][k] = v2;
                   B[j + 2][k] = v3;
                   B[j + 3][k] = v4;
                   B[j + 4][k] = v5;
                   B[j + 5][k] = v6;
                   B[j + 6][k] = v7;
                   B[j + 7][k] = v8;
               }
           }
       }
   }

这样就可以大量的减少MISS次数，这种方法理论上最少的MISS次数是256次，但是由于矩阵对角线位置的块会造成组冲突，所以对角线处的分的四个块，每一个快会多7次，也就是256+7x4=284次，加上系统的4次miss，就是我们得到的288次

64 x 64

说实话这一关比较难，想到了满分的办法但是不想去实现了，缓一缓凑合着过先。。。。

还是先假设将缓存全部填满需要多少行，在64的矩阵中只需要4行，所以如果在使用8 x 8的小矩阵分块的话在分块矩阵中都会造成组间冲突，所以退而求其次使用4 x 4的矩阵分块，这样做的坏处就是没有充分利用缓存，之使用了缓存块的一半内容，是达不到满分的，正确的做法是先分成8 x 8的矩阵，在使用一次分块技术将8 x 8的矩阵分成4个4 x 4的矩阵然后进行转置，当然这中间的过程有些复杂我就不想在说了（前面的这些东西搞懂都花了一天脑袋要炸了）。直接看4 x 4矩阵分块。

 int i, j, k, l;
 int v1, v2, v3, v4, v5, v6, v7, v8;
if (N == 64) {
        for (i = 0; i < N; i += 4) {
            for (j = 0; j < M; j += 4) {
                for (k = i; k < i + 4; ++k) {
                    v1 = A[k][j+0];
                    v2 = A[k][j+1];
                    v3 = A[k][j+2];
                    v4 = A[k][j+3];

                    B[j+0][k] = v1;
                    B[j+1][k] = v2;
                    B[j+2][k] = v3;
                    B[j+3][k] = v4;
                }
            }
        }
    }

61 x 67

这个说实话没有在细细的去计算去想了，非正方形矩阵最好的方式就是使用多个值去测试，然后选出一个最优解，这里的最优解法是分为17 x 17的矩阵。MISS率在1950左右

if (N == 67) {
        for (i = 0; i < N; i += 17) {
            for (j = 0; j < M; j += 17) {
                for (k = i; k < N && k < i + 17; ++k) {
                    for (l = j; l < M && l < j + 17; ++l) {
                        v1 = A[k][l];
                        B[l][k] = v1;
                    }
                }
            }
        }
    }

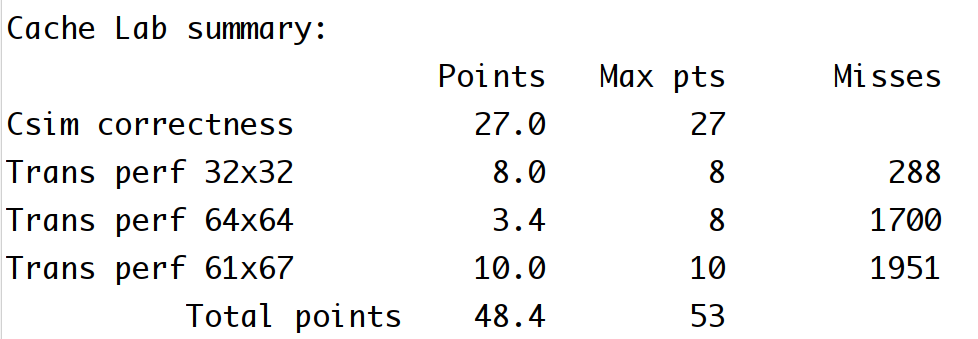
总结

最后结果也是没有拿到满分，但是还是收获了不少东西，那种想问题想不明白的感觉是真的痛苦，想明白了又觉得很爽。后面有时间还会会过头来继续优化这种类似的问题。还有就是读书一定要慢慢的读，这本csapp算是少数耐心慢慢读的书了，很多问题看不懂都会看好几遍甚至花几天时间来搞懂，算是收获不小，也领悟到了读计算机书籍的一些方法。